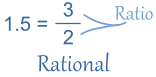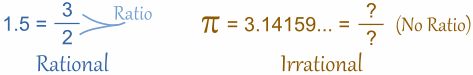సంవర్గ మానాలు

సంవర్గ మానాలను గూర్చి తెలుసుకోవడానికి ఒక చిన్న ప్రశ్న వేసుకొందాం

2 ను ఎన్ని సార్లు గుణిస్తే 8 వస్తుంది? 3 సార్లు. దీన్ని ఘాతాంక(exponent) రూపంలో వ్రాస్తే 2³=8

ఇందులో 2 ను భూమి(base) అని అంటారని మనకి తెలుసు. ఇపుడు 3 ను 2 భూమికి 8 యొక్క సంవర్గమానం అంటాము. దీన్ని logarithm అని చదువుతాము Log  అనే సంకేతంతో సూచిస్తాము.

log₂(8) = 3

ఇదే విధంగా

3ను ఎన్ని సార్లు గుణిస్తే 81  వస్తుంది? 4 సార్లు.  దీన్ని ఘాతాంక రూపంలో వ్రాస్తే 3⁴=81

ఇందులో 3  భూమి. ఇపుడు 4  ను 3  భూమికి 81  యొక్క సంవర్గమానం అంటాము. దీనిని వ్రాయాలంటే

  అని వ్రాస్తాము.

log₃(81) = 4

10 ని ఎన్ని సార్లు గుణిస్తే 100000  అవుతుంది ? 5 సార్లు.  దీన్ని ఘాతాంక రూపంలో వ్రాస్తే 10⁵=100000

ఇందులో 10   భూమి. ఇపుడు 5   ను 10   భూమికి 100000 యొక్క సంవర్గమానం అంటాము. దీనిని వ్రాయాలంటే

log₁₀(100000) = 5

  అని వ్రాస్తాము.

అంక గణిత ప్రాథమిక సిద్దాంతము

అంక గణిత ప్రాథమిక సిధ్ధాంతం ప్రకారం 1 కంటే పెద్దదైన ప్రతి పూర్ణ సంఖ్య ఒక ప్రధాన సంఖ్య కాని, ప్రధాన సంఖ్యల లబ్ధం గాని అయి ఉంటుంది.

దీని ప్రకారం ప్రధాన సంఖ్యలు సంఖ్యావ్యవస్థకు ఇటుకలలాంటివి . అంటే ఏ సంయుక్త సంఖ్య నయినా ప్రధాన సంఖ్య ల లబ్ధంగా వ్రాయవచ్చు.

క్రింది ఉదాహరణను గమనించండి 4 అనే సంయుక్త సంఖ్యను 2x2 గా వ్రాసాము.6 ను 2x3గా, 8 ని 2x2x2గా వ్రాయగలము. ఇక్కడ గమనించాలసిందేమిటంటే 4, 6, 8 లను ప్రధాన సంఖ్యల లభ్దంగా రాయచ్చు.

163800 ను 2x2x2x3x3x5x5x7x13 గా రాయవచ్చు.  

163800=2³ X 3²X 5²X7X13

ఇక అఁక గణిత ప్రాథమిక సిధ్దాంతాన్ని క్రింది విధంగా నిర్వచిస్తాము
నిర్వచనం: ప్రతి సంయుక్త సంఖ్యను ప్రధానాంకాల లబ్ధంగా రాయవచ్చు. మరియు ప్రధానాంకాల క్రమం ఏమైనప్పటికీ ఈ కారణాంకాల లబ్ధం ఏకైకము.

x ను ఒక  సంయుక్త సంఖ్య గా తీసు కోండి. దీనిని మనం సాధారణంగా x =p1,p2,p3………..గావ్రాయ వచ్చు. ఇందులోp1,p2,p3 లను ఆరోహణ క్రమంలో ఘాతాల రూపంలో  వ్రాసామనుకోండి. ఆ లబ్ధం ఏకైకమవుతుంది. అంటే పై ఉదాహరణలో 163800 ను ప్రధాన కారణాంకాల లబ్ధంగా ఎలా  వ్రాసినప్పటికి చివరికి వాటిని  ప్రధానకారణాంకాలుగా వ్రాసి, ఆరోహణ క్రమంలో ఘాతాల రూపంలో వ్రాయ గలిగే విధానం ఒక్కటే.

కసాగు : 

రెండు కాని అంతకంటే ఎక్కువ సంఖ్యలకు అతిచిన్న గుణిజాన్ని  ఆ సంఖ్యలకు కనిష్ట సామాన్య గుణిజము  అంటాము. 

3,5 లకు గుణిజాలు 

3 గుణిజాలు : 3,6,9.12,15, 18,21,24,27,30,. . . . . .

5 గుణిజాలు: 5,10, 15, 20, 25, 30,.... 

పై రెండు సంఖ్య లకు గుణిజాలలో రెంటికి చెందిన గుణిజాలు గుర్తిస్తే 15, 30 వస్తాయి. (సామాన్య గుణిజాలు)

ఇందులో చిన్న సామాన్య గుణిజమేది ? 15 కనుక 15 ను, 3,5 ల కనిష్ట సామాన్య గుణిజం అంటాము. ఆంగ్లంలో LCM అని అంటారు.  క్రింద ఇంకా వివరంగా పట రూపంలో చూపడం జరిగింది.

గసాకా:

రెండు కాని అంతకంటే ఎక్కువ సంఖ్యలను కారణాంకాలుగా విభ జించినప్పుడు ఆ సంఖ్యలకు ఉన్న ఉమ్మడి కారణాంకాలలో అతి పెద్ద కారణాంకం ను గసాకా అంటారు.

15, 30 ,  105 ల కారణాంకాలను పరిశీలిద్దాం.

15 కారణాంకాలు 1, 3,5, మరియు15

30  కారణాంకాలు 1, 2, 3, 5, 6, 10, 15 మరియు 30

105  కారణాంకాలు 1, 3, 5, 7, 15, 21, 35 మరియు  105

15, 30, 105 ల కు సామాన్య కారణాంకాలు  1, 3, 5 and 15

ఇందులో అతిపెద్దది 15

కనుక 15 ను గరిష్ట సామాన్య కారణాంకం అంటాము.

కసాగు, గసాకా ల మధ్య సంబంధం:

a మరియు  b లు రెండు ధన పూర్ణ సంఖ్యలు అయునచో వాటి గసాకా X కసాగు = a.b అవుతుంది. 

క్రింద ఖాన్ అకాడమీ వారు  ప్రధాన సంఖ్యలు పైన తెలుపుకున్న అంక గణిత ప్రాథమిక సిధ్ధాంతం పై వీడియోనుంచారు. దయ చేసి చూడండి.

 https://www.youtube.com/watch?v=8CluknrLeys

Prime Numbers Up To 100

పదవ తరగతి గణితం - వాస్తవ సంఖ్యలు

పరిచయం:

కరణీయ సంఖ్యలు అకరణీయ సంఖ్యలు కలసి ఉన్న సమూహాన్ని వాస్తవ సంఖ్యలు అంటారు.
వాస్తవ సంఖ్య ల సమితి క్రింద చూపిన విధంగా ఉంటుంది.

మరి అకరణీయ సంఖ్యలు అంటే ఏమిటి?

అకరణీయసంఖ్యలు 

అకరణీయ సంఖ్యలను p/q రూపంలో వ్రాయగలిగే సంఖ్యలు ఇందు p ,q లు పూర్ణ సంఖ్యలు

q≠0

ఇవి పూర్ణ సంఖ్య ల సమూహం కన్నా పెద్దది.

అన్ని అకరణీయ సంఖ్యలను అంతమయ్యే దశాంశాలు లేదా అంతం కాని దశాంశాలు గా వ్రాయవచ్చు.

ఉదాహరణ కి 1,2,3 లు అకరణీయ సంఖ్యలు వీనిని 2/1, 3/1, 4/1 రూపంలో వ్రాయగలం.

అలాగే 6.25, 6.45 లను 625/100, 645/100 (p/q)  రూపంలో వ్రాయ గలం.

ఆవర్తన దశాంశాలయిన ఈ క్రింది సంఖ్యలను కూడా p/q రూపంలో వ్రాయ గలం. కనుక ఇవి అకరణీయ సంఖ్యలు.

3.3333333....  , 7.127127127........... ,
Example:

1.5 ఒక అకరణీయ సంఖ్య ఎందుచేత ?
 1.5 = 3/2 (1.5 ని భిన్న రూపంలో వ్రాయగలిగాం )

ఇంకా కొన్ని ఉదాహరణలు

సంఖ్య	p/q రూపంలో	అకరణీయ సంఖ్య ?
5	5/1	అవును
1.75	7/4	అవును
.001	1/1000	అవును
0.111...	1/9	అవును
√2 (square root of 2 రెండు యొక్క వర్గ మూలం)	?	కాదు  !

చివరి సంఖ్య ను మనం  p/q రూపంలో రాయలేక పోతున్నాం ఇలాంటి సంఖ్యలు మన సంఖ్యా వ్యవస్థ లో ఇంకా ఉన్నాయి, అలాంటి సంఖ్యలను కరణీయ సంఖ్యలు అంటాము. ఉదాహరణకి, √5,√7,√6  
ఇంకా ఈ జాబితాలోకి వచ్చే సంఖ్యలు మరి కొన్ని Pi (π).
Pi (π) = వృత్త పరిధి / వ్యాసము  అని మనకి తెలుసు.

Pi (π) =వృత్త పరిధి / వ్యాసము

కరణీయసంఖ్యలు 

మరి ఈ కరణీయ సంఖ్యలు అంటే ఏమిటో చూద్దాం:

ఏ సంఖ్యలను p/q రూపంలో రాయలేక పోతున్నామో ఆ సంఖ్యలను కరణీయ సంఖ్యలు అంటారు. 

Examples:

ఉదాహరణ   √5,√7,√6  
ఇంకా ఈ జాబితాలోకి వచ్చే సంఖ్యలు మరి కొన్ని Pi (π), e (Euler's Number), Golden Ratio,
Pi (π)

π = 3.1415926535897932384626433832795 (ఇంకా....... ) Pi. విలువను మనం భిన్న రూపంలో వ్రాయలేము

 Pi.=²²/₇ = 3.1428571428571... అని మనం తీసుకొనే విలువ కొంత దగ్గరి విలువ అది ఖచ్చితం కాదు.

కొన్ని గుర్తుంచుకోవలసిన కరణీయ సంఖ్యలు : 

	Pi విలువ ఒక కరణీయ సంఖ్య దీని విలువ లో ఆవర్తన దశాంశాలు ఇప్పటి వరకు కనుగొనబడలేదు. 3.1415926535897932384626433832795 (and more ...)
	e (Euler's Number) అనేది ఒక కరణీయ సంఖ్య దీని విలువ లో ఆవర్తన దశాంశాలు ఇప్పటి వరకు కనుగొనబడలేదు. e = 2.7182818284590452353602874713527 (and more ...)
	Golden Ratio అనేది ఒక కరణీయ సంఖ్య దీని విలువ= 1.61803398874989484820... (and more ...)
	అనేక సంఖ్యల వర్గ మూలాలు, ఘన మూలాలు, మూలాలు కరణీయ సంఖ్యలవుతాయి : √3 1.7320508075688772935274463415059 (etc) √99 9.9498743710661995473447982100121 (etc) కాని అన్ని సంఖ్యల మూలాలు కరణీయ సంఖ్యలు కావు. ఖచ్చిత మూలం లేనివి మాత్రమే కరణీయ సంఖ్యలు
ఉదాహరణకి √4 = 2 ( అకరణీయ సంఖ్య), మరియు  √9 = 3 ( అకరణీయ సంఖ్య) ...

 కరణీయ సంఖ్యల గురించి ఒక చిన్న విషయం: 

క్రింద చూడండి :

• π × π = π² కరణీయ సంఖ్య
• But √2 × √2 = 2 కరణీయ సంఖ్య కాదు 

కనుక కరణీయ సంఖ్య ల లబ్ధం కరణీయ సంఖ్య యే అవాల్సిన పనిలేదు.

వాస్తవ సంఖ్యలను సంఖ్యా రేఖ పై చూపడం:

అకరణీయ సంఖ్యలను సంఖ్య లను సంఖ్యా రేఖ పై చూపగలం:

మరి కరణీయ సంఖ్య లను చూపగలమా ?